Free CFA Certification Practice Questions:
 Exhibit 1
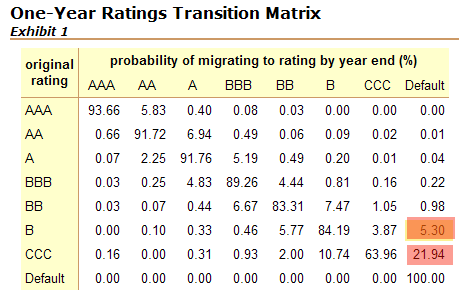
indicates a ratings transition matrix. constructed by Standard & Poor's.
It indicates one-year ratings migration probabilities based upon bond rating
data from the period 1981-2000.
Exhibit 1
indicates a ratings transition matrix. constructed by Standard & Poor's.
It indicates one-year ratings migration probabilities based upon bond rating
data from the period 1981-2000.

A portfolio consists of 30 percent B and 70 percent CCC-rated bonds. If a randomly selected bond defaults in one year, what is the probability that it was a CCC-rated bond?
A) 9.38%
B) 90.62%
C) 16.95%
-
[Ans: B]
We can use Bayes rules as follows:
P(CCC-rated Bond | Default) = P(Default | CCC-Rated Bond) * P(CCC-Rated
Bond) / P (Default)
P(Default | CCC-Rated Bond) = 21.94% (from the transition matrix)
P(CCC-Rated Bond) = 70% (CCC-rated bond are 70% of portfolio)
P(Default) = P(Default | B-rated) * P(B-rated) + P(Default | CCC-rated) *
P(CCC-rated)
= (5.30% * 30%) + (21.94% * 70%)
= 16.95%
P(CCC-rated Bond | Default) = P(Default | CCC-Rated Bond) * P(CCC-Rated Bond) / P (Default)
= 21.94% * 70% / 16.95%
= 90.62%
BACK | NEXT





